为什么NumPy这么快

NumPy是使用 Python 进行科学计算的基础包，是Python数据科学基础中的基础。它具有下面六大特点:

1. 强大的 N 维数组。NumPy 向量化、索引和广播概念快速且通用，是当今数组计算的实际标准。
2. 数值计算工具。NumPy 提供全面的数学函数、随机数生成器、线性代数例程、傅里叶变换等。
3. 可互操作。NumPy 支持广泛的硬件和计算平台，与分布式、GPU 和稀疏数组库配合良好。
4. 高性能。NumPy 的核心是经过良好优化的 C 代码。享受 Python 的灵活性和编译代码的速度。
5. 使用方便。NumPy 的高级语法使任何背景或经验水平的程序员都可以轻松访问并提高效率。
6. 开源。NumPy在自由BSD 许可下分发，由充满活力、响应迅速且多样化的社区在 GitHub 上公开开发和维护。

以上来自NumPy的官网，个人觉得NumPy主要具有下面二个特点，我们一起来了解它:

1. 高性能
2. API简单易用

高性能的NumPy

高性能是科学计算的首要需求，大量数据，大量的循环，快字当先，毕竟谁也不希望跑一个模型好几天。我们先看一个简单的例子: 使用Python的列表推导式输出长度1000的数组，每个元素是自然数的平方, 代码如下:

1
2

L = range(1000)
%timeit [i**2 for i in L]

这是使用NumPy的方式:

1
2

a = np.arange(1000)
%timeit a**2

测试结果中两者的耗时如下表:

可以看到测试结果NumPy比列表推导式快了几百倍。

为什么NumPy这么快呢？首要原因在于NumPy的核心是经过良好优化的C代码，具有编译代码的速度。其次在于NumPy的数据结构设计和算法，这一点是很多文章都没有介绍的，这是我想重点介绍的内容。

NumPy提供的最重要的数据结构是一个称为NumPy数组的强大对象，它有下面两个特点:

1. 数组长度固定
2. 仅支持同类型数据元素

我们知道Python的list，是动态的并且可以存放任意类型的元素, 比如:

1
2
3
4

>>> a = ["a", 9, 9.0, True]
>>> a.append("b")
>>> a
['a', 9, 9.0, True, 'b']

a数组包含了4个元素，数据类型各不相同，我们还可以使用append方法往a中添加元素。实际数组有长度(length)和容量(capacity)两个概念，我这里借用一下go-slice的图示意一下:

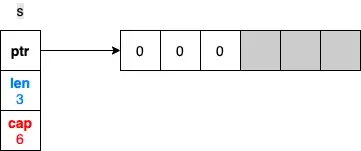
• 长度表示当前数组内元素个数
• 容量表示当前数组最多可以存储多少个元素，超过了则需要重新申请内存区域
• 一般扩容申请都会翻倍。比如上图是6个方格，已经使用了4个，再添加3个，这时候会直接再申请6个，而不是3个。

所以我们可以设想一下，使用列表推导式的时候，经过多次的内存申请，效率就低了下来。而NumPy数组是长度固定的，一次申请到位，自然效率会高不少。

如果大家做过协议处理，一定理解定长和不定长协议。定长协议中，每个协议长度相同，计算起来非常快捷，直接当前位置+固定长度就可以获取下一个协议位置；而不定长协议，还需要解析当前协议长度，判断当前协议的长度，才可以得知下一个协议的位置。

我们把数组在内存中的存储相信成协议的字节流，这就一致了。NumPy仅支持同类型的数据元素，就是定长协议的解析，效率很高。

1
2
3
4
5
6
7
8
9

# 定长
+---+---+---+---+---+---+
|   |   |   |   |   |   |
+---+---+---+---+---+---+

# 不定长
+--+----+------+--+-----+
|  |    |      |  |     |
+--+----+------+--+-----+

• 字符图不好理解的话，大家可以把定长元素想象为高铁车厢，不定长元素想象成汽车，那么春运的铁路运输和公路运输效率就一目了然

需要注意，NumPy中数组也可以放不同 Python类型 元素，但是它们都会(长度)向上对齐到 NumPy数据类型 ，下面的U32就是NumPy的数据类型:

1
2

np.array(["a", 9, 9.0])
array(['a', '9', '9.0'], dtype='<U32')

NumPy支持矩阵运算，这也是NumPy高性能原因所在。

我们先复习一下矩阵的哈达玛积(Hadamard product)，使用符号A⊙B表示：

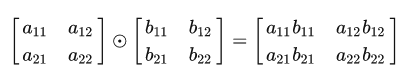
• 两个矩阵对应位置的元素逐一相乘

那么a**2的运算使用矩阵的方式就是这样:

1
2
3

+-----------+     +-----------+     +--------------+
|1,2,3,...,n|  ⊙  |1,2,3,...,n|  =  |1,4,9,...,N*N |
+-----------+     +-----------+     +--------------+

• 这里二维变成一维，计算法则是一样的

使用矩阵后就可以进行并发处理了，这和大数据中的map-reduce模型类似。我们可以这样理解它，普通的列表推导式:

1
2
3

L = range(1000)
for i in L:
    i**2        

需要经历1000次循环，并且只能够在CPU的单核上逐次执行。根据矩阵运算公式，对应A_i位置的元素，只需要和B_i位置的元素相乘，和其它的999个数都无关，那么我们可以将整个大的运算拆分成1000个小运算，分到多个CPU核上并发执行，计算出每个位置元素后，再汇总即可。

所以NumPy采用良好的数据结构+高效的算法，性能自然上去了。

简单易用的NumPy

如果仅关注性能那么Fortran, matlab, R语言也足够了，或者直接使用C语言。Python语言足够简洁和灵活，使用它包装的API简单易用，又使NumPy的开发效率带来很大提升。我们可以通过下面几个小的例子来了解NumPy的这个特点。

首先是NumPy的数组切片非常强大，如图:

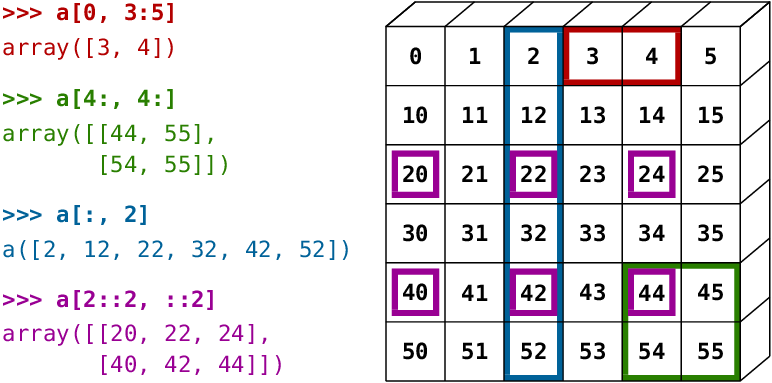
• 红色切片取第0行的，第3-第4个元素(左闭右开)
• 绿色切片取第4行和第4列后面的元素
• 蓝色切片取第3列
• 紫色切片按照2的步进取元素

然后是NumPy支持数学运算:

1
2
3
4
5
6

>>> import numpy as np
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> np.sin(a)
array([ 0.        ,  0.84147098,  0.90929743,  0.14112001, -0.7568025 ])

同样的计算，我们在python中大概这样实现:

1
2
3
4
5

import math
>>> import math
>>> items = [0, 1, 2, 3, 4]
>>> list(map(lambda x: math.sin(x), items))
[0.0, 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079282]

对比可见，NumPy包装的API更便捷。

最后NumPy还提供了很多统计函数， 比如:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

>>> x = np.array([1, 2, 3, 4])
>>> np.sum(x)
10
>>> x.sum()
10
>>> x.max()
4
>>> x.min()
1
>>> x.mean()
2.5

• np.sum(x) 和 x.sum() 是API的两种写法，我们更常使用后面的方法

更多的API使用，可以阅读参考链接中的用户指南和参考手册

小结

NumPy由于高性能和简单易用，是Python进行科学计算的基石。本文从NumPy的数据结构和算法实现上，探讨了其高性能的原理，并简单介绍了部分API，希望能吸引你学习它的兴趣。

参考链接

• https://www.numpy.org.cn/user/
• https://www.numpy.org.cn/about/