从零开始机器学习 - 白话机器学习

ChatGPT大火，大家都在跟踪这个热点。概念股在市场大火，相关不相关的公司都宣称要做AI；全网都在发布教程教你如何注册账号，如何利用ChatGPT洗稿，获取流量 …；传统行业的朋友，也找我打听，感觉它能够解决他们的痛点。但是人类总是会高估一项技术的短期价值，而低估其长期价值。现在通过它已经赚到钱的人，属于眼光敏锐的；还没有赚到钱或还没有解决问题的人，几天后会大概失去兴趣。做技术的不如冷静下来好好了解一下其底层应用的机器学习技术，了解一下实现原理，投资一下其长期价值。

机器学习是一门开发算法和统计模型的科学，计算机系统使用这些算法和模型，在没有明确指令的情况下，依靠既有模式和推理来执行任务。计算机系统使用机器学习算法来处理大量历史数据，并识别数据模式。这可让计算机系统根据给出的输入数据集更准确地预测结果。

以上是机器学习的定义，如果没有读懂也没有关系，记住几个加粗的关键字就行, 下面我们一起来花几分钟时间来学习它。本文不会介绍太多的数学知识，有高中数学基础就可以放心大胆的食用。

回归问题

回归分析(Regression Analysis)是一种统计学上分析数据的方法，目的在于了解两个或多个变数间是否相关、相关方向与强度，并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。简单的说就是通过一些已知的历史数据，推测出数据x和y之间的函数关系y=f(x),那么对于某个新的 x' , 我们可以利用函数公式计算(预测)其对应值y'。但是和解方程不同，这里的y'是不精确的，会和真实值之间存在偏差。

让我们具体看一个例子，拿国民话题的房子来说。现在我手里有一栋房子需要售卖，我应该给它标上多大的价格？房子的面积是90平米，价格是300万，290万，还是340万？很显然，我希望获得房价与面积的某种规律。那么我该如何获得这个规律？用报纸上的房价平均数据么？还是参考别人面积相似的？无论哪种，似乎都并不是太靠谱。

我调查了周边与我房型类似的一些房子，获得一组数据。这组数据中包含了大大小小房子的面积与价格，如果我能从这组数据中找出面积与价格的规律，那么我就可以得出房子的价格：

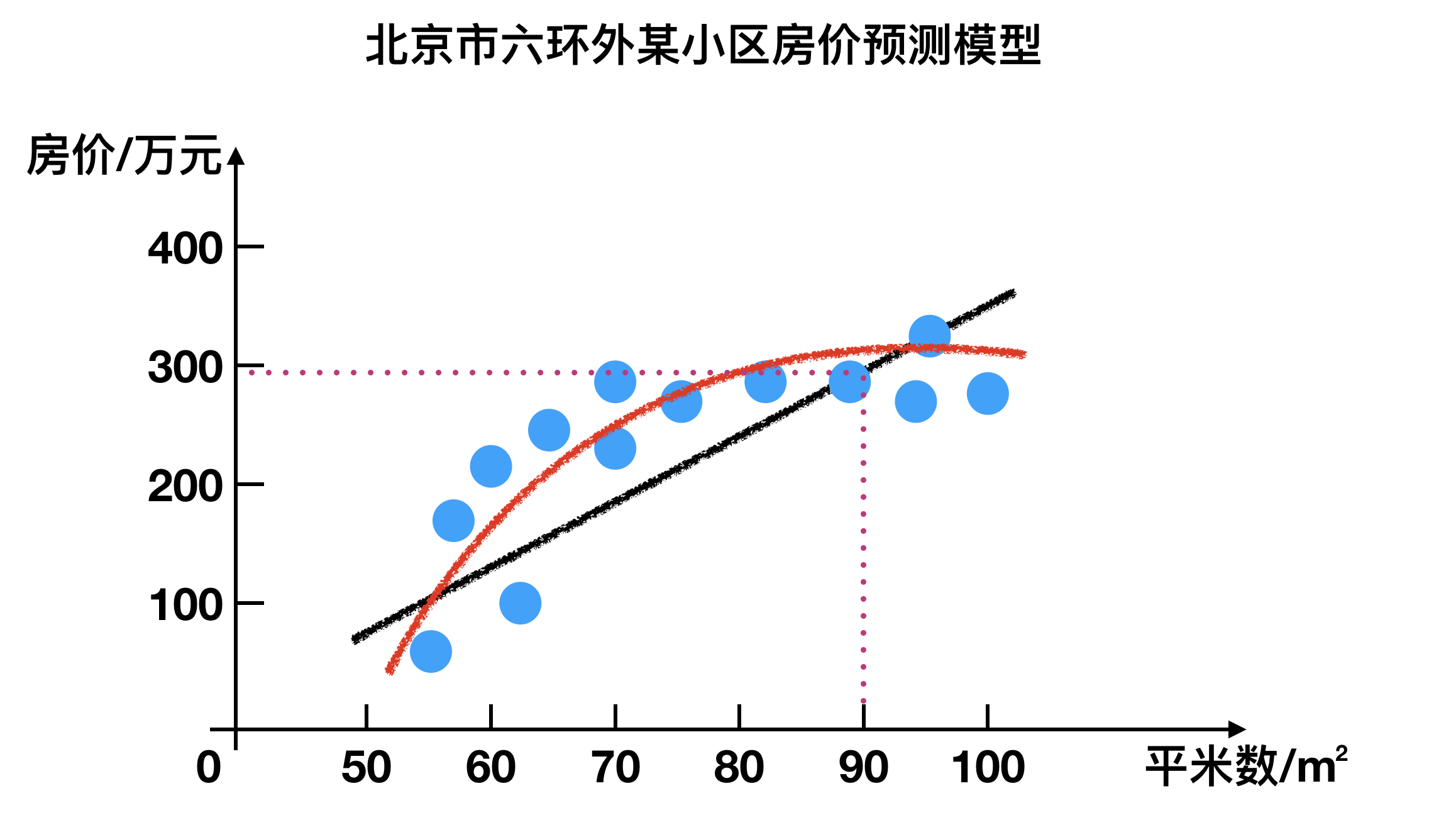
利用已有的蓝色点，我们可以画一条黑色的直线来贴合(拟合)它们，也可以使用一条红色的曲线来贴合(拟合)它们。假设我们使用直线吧，简单一些。这条直线可以表示为 y=wx+b, 这样90平米的房子，带入公式就可以知道其价格。显然房价不只是和面积相关，楼层，位置，朝向等等都会影响房子的价格，不过没有关系我们先从最近简单的问题开始着手。

房价预测问题现在被我们简化为查找一个合适的线性方程的数学问题。这样简化后的模型，我们还可以用来处理类似问题，比如年龄和身高的推断问题，这是没有明确指令的含义，也是机器学习的强大之处。

如何查找一个合适的线性方程呢？这就需要用到最小二乘法了。我们可以进一步把数据抽象成下图:

4个红色的数据和1条蓝色的直线 y=wx+b, 对应每个 x，都有真实值 y和预测值 y'。我们可以想象一下，将蓝色的直线上下平移或者左右旋转一个角度，都可以拟合4个红色的数据点，那么这一堆的直线中那条直线是最合适的呢? 最小二乘法定义使每个预测值和真实值之间的平方和最小的直线就是最优直线。这里复杂的数学证明我们可以先忽略，把它当做定理即可。

这样查找一个合适的线性方程的数学问题，进一步转换为求极限值的问题。这个极限问题可以表示为求下面函数的极值:

1

g=(y-y')=(w'x+b'-wx-b)^2=((w'-w)x+(b'-b))^2

省略掉w和b后，可以归纳为:

1

g(x)=x^2

显然根据x^2的图像，我们可以知道，函数的导数为零的地方就是函数的极值:

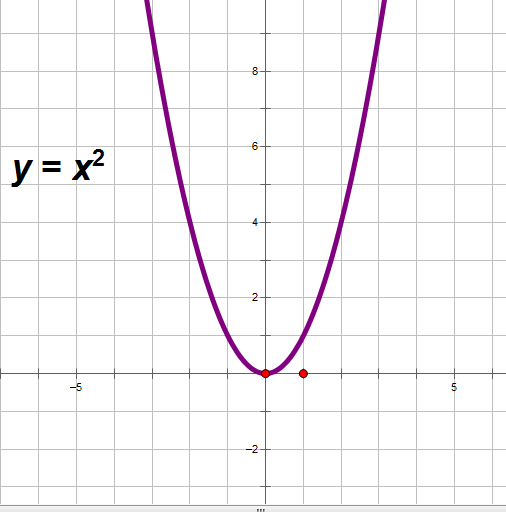
到此求极值的问题又变成函数求导数，这是机器学习中回归问题的数学原理。

分类问题

分类问题是机器学习可以处理的第二类问题。假设有肿瘤样本数据如下图:

图中x轴表示肿瘤大小，y轴表示患者的年龄，肿瘤的良性和恶性使用性状和颜色区分。我们同样可以在平面上画一条直线，将良性肿瘤和恶性肿瘤区分开来，直线下方的是良性，直线上方的是恶性。当然数据也会有误差，各有一个良性和恶性被误判了，这需要医生进一步确认。

和房价问题一样，我们把数据抽象一下，形成下面的图形:

因为这里x和y没有相关性，所以我们更习惯称为x1和x2轴

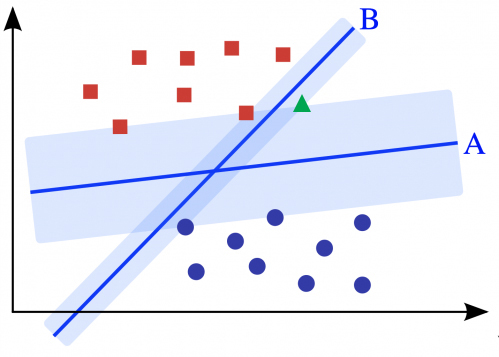
从左图我们可以知道，在平面上一样有很多条直线可以将数据区分开，那么那条直线会是最优的呢? 这时候轮到支持向量机(SVM)登场了。

支持向量机会找到最好的那条线，这条线满足到两类数据的边界形成的间距最大。数学证明，我们一样略过。但是我们可以这样理解这个问题, 边界越大，表示可以冗余的 未知 数据越多。因为机器学习是使用样本数据来对未知数据进行预测，那么在样本空间中留下的空间越大，对未知数据的接纳能力越强，分类的准确性越高，比如下图A形成的空间:

回归和分类

前面介绍了使用线性回归算法预测房价和使用支持向量机区分肿瘤，其中对于房价的预测结果是连续的，而肿瘤区分结果是离散的。实际上这两类问题是可以互通的，这时候需要使用到Sigmoid函数，它的公式如下:

1

f(x)=\dfrac{1}{1+e^{-x}}

公式比较难以理解，但是Sigmoid图像很简单，可以把任意数值映射到[0,1]的区间:

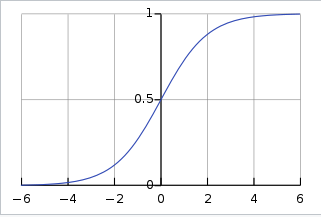
这对IT的同学应该都不陌生，网卡的电讯号转换成比特也和这没差别。

机器学习和经典编程的差异

决策树算法可以比较好的展示机器学习和经典编程的差异。我们希望实现一个挑选好瓜和坏瓜的程序，已知的一些经验数据如下表:

从表中我们可以看到，可以通过色泽，根蒂形状，敲声等六个因素去帮助判断是好瓜还是坏瓜。在经典编程中，我们会分析数据，提取规则。比如看起来纹理清晰的是好瓜会更高概率，脐部凹陷和触感硬滑是好瓜的概率也更高一些。我们编写最简单的程序可能如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def good_or_bad(watermelon):
    # 默认坏瓜
    flag = 0
    if watermelon["纹理"] == "清晰" and watermelon["纹理"] == "清晰":
        flag = 1
    elif watermelon["敲声"] == "浊响" and watermelon["触感"] == "硬滑":
       flag = 1 
    ...
    else:
        ...
    return flag

watermelon={"色泽":"青绿","根蒂":"蜷缩","敲声":"沉闷","纹理":"稍糊","脐部":"稍凹","触感":"硬滑"}

在机器学习中，大概的程序如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

from sklearn import tree

Xtrain, Ytrain = [(青绿,蜷缩,浊响,清晰,凹陷,硬滑),(乌黑,蜷缩,沉闷,清晰,凹陷,硬滑),...],[1,1,...]

Xtest,Ytest = (青绿,蜷缩,沉闷,稍糊,稍凹,硬滑), 0

clf = tree.DecisionTreeClassifier(criterion="entropy") 
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest) #返回预测的准确度
score
# 0.7

这段伪代码的逻辑是:

• sklearn是python的一个开源的机器学习包
• Xtrain和Ytrain是我们的训练数据集，分表表示瓜的特征(属性)数据以及瓜的好坏
• Xtest和Ytest是我们的测试数据
• DecisionTreeClassifier是一个决策树算法
• clf = clf.fit(Xtrain, Ytrain) 我们使用测试数据训练算法，得到一个识别瓜好坏的模型
• clf.score(Xtest, Ytest) 用来测试某个瓜的准确度(概率)，这里我们这个瓜是坏瓜的可能性是0.7

当然实际的情况会比这里的伪代码更复杂，会涉及参数优化等。不过我们可以清楚的看到两种编程方式的两个差异。

1. 在机器学习中，我们不需要理解具体的业务，并把业务翻译成代码，只需要把数据丢给算法，优化参数，让机器去发现数据中的规律。
2. 在经典编程中，我们会返回这个瓜是好瓜还是坏瓜，虽然判断会不正确，但是还是会给出明确的是和否的结论，在机器学习中则是返回模糊的结果，某种可能性(概率)。

小结

机器学习算法可以通过历史数据的学习(分析)，对未知数据进行预测。机器学习可以处理回归和分类两类问题，并且这两类问题可以转换。线性回归算法可以处理回归问题，支持向量机可以用于分类问题，这是两种有较好解释性的监督学习算法。机器学习算法的编程方式和经典编程方式不一样，它是面向数据的，而不是精确指令(规则)的，可以得到有偏差的结果。

参考链接

• 什么是机器学习？
• 最小二乘法
• 梯度下降
• 支持向量机 (SVM) 的解析与推导
• 吴恩达2022机器学习
• 李航《统计学习方法》
• 周志华《机器学习》